题解【NOI Online #2 提高组】涂色游戏

题目链接

题意简述

有两个数$a\le b$，给出$k$，问是否存在$mb<na<(n+1)a<\cdots (n+k-1)<(m+1)b,(m+1)b<10^{20},m,n\in N,n\ge 1$。存在输出“NO”，不存在输出“YES”（由于转换了求的东西所以存在和不存在与原题输出相反）。

题解

先说一下为什么这么化简题意。原题中的$p_1,p_2$这里用$a,b$表示。不妨设$a\le b$，则染色的情况必定为$a\cdots aba\cdots aba\cdots$的情形。可以发现，相当于是$b$在截断$a$的连续染色。而为了实现原题中不超过k个连续的愿望，$lcm(a,b)$显然要染成$b$去防止$a$的延伸。接下来只需要看是否在$10^{20}-1$的范围内，每个$b$之间间隔的$a$的数量都小于k。当然，首先要特判$k=1$的情况。

接下来讲一下我的解题思路。一开始是想至少搞一个下界出来，即：假设每个$b$之间夹的$a$的数量最多为$c$，则$c\ge \lfloor\frac{b-1}{a}\rfloor$，也就是一开始$0\thicksim b$中存在的$a$的数量。仔细想想，由于$b-1=\lfloor\frac{b-1}{a}\rfloor+r,0\le r < a$，如果想在两个$b$地倍数之间的a开头往前或结尾往后扎扎实实地再塞进一个$a$是不可能的，想要再添加只有可能是存在一个数$\lambda,mb<\lambda< mb+r$。这样好像讲的有点乱,看图明白一点：

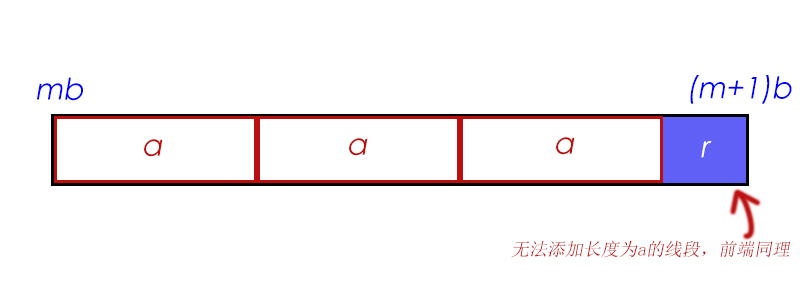
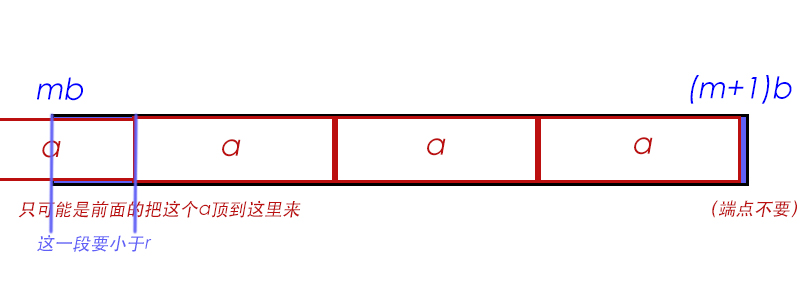
截取线段和什么类似？取模！若$\lambda$存在，则不可避免的最多颜色连续数为$\lfloor\frac{b-1}{a}\rfloor+1$，不然，则为$\lfloor\frac{b-1}{a}\rfloor$。即为判定$ax\equiv t(mod\ b)(0\le t<r)$是否有解。进一步的，判定$ax+by=t$是否有解。又由裴蜀定理知，该方程有解的充要条件为$\gcd(a, b)|t$。且$r$可以取遍$0\thicksim r-1$的整数，所以只需判断$r$和$\gcd(a, b)$的大小关系。如此一来，只需将最多颜色连续数和$k$进行比较，若$k$比较大则有解，否则无解。本题就得到了解决。特殊地，当$a|b$时$r=0$，此时是可以不让$b$染成$a$的，代入发现同样可以通过比较$r$与$\gcd(a,b)$的大小关系获得正确答案。

等等，我们还有个范围问题！怎么确定如此找到的$(m+1)b$是否小于$10^{20}$呢？设$d=\gcd(a,b)$，由于$ax+by=t$的解集与$\frac{a}{d}x+\frac{b}{d}y=\frac{t}{d}$相同，不妨先设$a\bot b$。
先证明一个引理：当$a\bot b$时，$\{0,a,2a,\cdots,(b-1)a\}$构成$b$的完全剩余系。
首先，$\{0,a,2a,\cdots,(b-1)a\}$和$\{0,1,2,\cdots,b-1\}$在元素个数上相同。下用反证法证明原集合中元素对$b$取模结果两两不同即可。
若$ax\equiv ay(mod\ b)(0\le x,y <p,x\neq y)$，且$a\bot b$，则$x\equiv y(mod\ b)$。进一步的，由于$0\le x,y <p$，则$x=y$，得出矛盾。
证毕。

这一步是想说明，只要有解，解的范围就在$[0,b/d-1]$中。而$mb<ax+t\le a(b-1)+a=ab,(m+1)b<ab+b\le 10^{18}+10^9<10^{20}$。
这回是真的结束了。

代码：

#include <cstdio>
#include <cctype>
char ans[2][10]={"NO\n", "YES\n"};

int gcd(int a,int b) {return b?gcd(b, a%b):a;}
int read()
{
	int res=0;
	char ch=getchar();
	while(!isdigit(ch))	
		ch=getchar();
	while(isdigit(ch))
		res=res*10+ch-'0',ch=getchar();
	return res;
}
int main()
{
	int T=read();
	while(T--)
	{
		int a=read(),b=read(),k=read();
		if (a>b)
			a^=b^=a^=b;
		if (k==1)
			printf("%s",ans[0]);
		else
		{
			int d=gcd(a, b),r=b%a;
			int s=(b-1)/a+(r>d);
			printf("%s",ans[s<k]);
		}
	}
	return 0;
}