最长不下降子序列

第一问，求出最长不下降子序列长度$s$。我知道你会用$O(nlogn)$的复杂度求它，但是仔细想想，这么做以后，后面怎么建图呢？我怎么知道两个点是否都在最长的不下降子序列上呢？回想一下朴素的$O(n^2)$的做法，状态$f_i$表示以$a_i$结尾的最长子序列长度。假如$i\le j,a_i\le a_j,f_i+1=f_j$，说明$f_j$是由$f_i$转移而来的，进而说明在以$a_j$结尾的最长不下降子序列的前一位可以是$a_i$。

第二问，限制每个点只能用一次，求最长不下降子序列数目。这里需要拆点，为了防止出现以下情况：

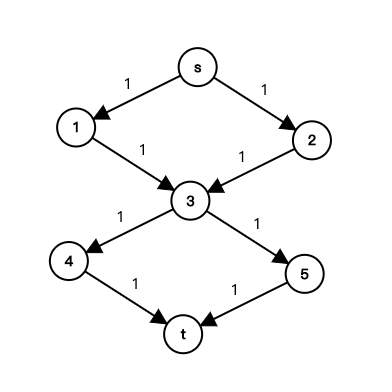
只需要加上一个虚点限制该点的出流只能为1，即可解决：

考虑源点与$f_i=1$的点相连，$f_i=s$的点与汇点相连；点与点之间根据上述转移条件连边。将所有边的边权都设为1。这样，从$s$到$t$的单位流量就表示存在1个经过的每个点只用1次的合法方案，每条路径之间一定不会有交点。

第三问，由于$x_1$和$x_n$可以重复使用，且它们只能作为第一个或最后一个存在于序列中，所以若它们与源点或汇点之间有连边，将边权设为$inf$即可。

代码：

#include <cstdio>
#include <cstring>
const int maxn=500+10;
const int maxm=1e6+10;
const int INF=0x3f3f3f3f;
int a[maxn],f[maxn],dep[maxn<<1];
int cur[maxn<<1],head[maxn<<1],to[maxm],nxt[maxm],val[maxm];
int tot=1,cnt=0;
int n,s,t;
struct Queue
{
	int a[maxn<<1];
	int l,r;
	Queue() {l=1,r=0;}
	void push(int x) {a[++r]=x;}
	void pop() {l++;}
	int front() {return a[l];}
	bool empty() {return l>r;}
}q;

int min(int x,int y) {return x<y?x:y;}
int max(int x,int y) {return x>y?x:y;}
void add(int u,int v,int w)
{
	nxt[++tot]=head[u];
	head[u]=tot;
	to[tot]=v;
	val[tot]=w;
}
bool bfs()
{
	memset(dep, 0x3f, sizeof(dep));
	dep[s]=0;
    q=Queue();
	q.push(s);
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for (int i=head[u];i;i=nxt[i])
		{
			int v=to[i];
			if (val[i]&&dep[v]>dep[u]+1)
			{
				dep[v]=dep[u]+1;
				q.push(v);
			}
		}
	}
	return dep[t]!=INF;
}
int dfs(int u,int minf)
{
	if (u==t||!minf)
		return minf;

	int used=0;
	for (int &i=cur[u];i;i=nxt[i])
	{
		int v=to[i];
		if (val[i]&&dep[v]==dep[u]+1)
		{
			int flow=dfs(v, min(minf-used, val[i]));
			if (!flow)
				continue;
			used+=flow;
			val[i]-=flow;
			val[i^1]+=flow;
			if (used==minf)
				break;
		}
	}
	return used;
}
int main()
{
	scanf("%d",&n);
	s=0,t=2*n+1;
	for (int i=1;i<=n;i++)
		scanf("%d",&a[i]);
	for (int i=1;i<=n;i++)
		f[i]=1;
	int sum=1;
	for (int i=1;i<=n;i++)
		for (int j=i-1;j>=1;j--)
			if (a[j]<=a[i])
				f[i]=max(f[i], f[j]+1);
	for (int i=1;i<=n;i++)
		sum=max(sum, f[i]);
	if (sum==1)
	{
		printf("%d\n%d\n%d\n",sum,n,n);
		return 0;
	}
	printf("%d\n",sum);
	for (int i=1;i<=n;i++)
	{
		add(i, i+n, 1),add(i+n, i, 0);
		if (f[i]==1)
			add(s, i, 1),add(i, s, 0);
		if (f[i]==sum)
			add(i+n, t, 1),add(t, i+n, 0);
		for (int j=i+1;j<=n;j++)
			if (a[i]<=a[j]&&f[i]+1==f[j])
				add(i+n, j, 1),add(j, i+n, 0);
	}
	int ans=0;
	while(bfs())
	{
		for (int i=s;i<=t;i++)
			cur[i]=head[i];
		ans+=dfs(s, INF);
	}
	printf("%d\n",ans);
	ans=0;
	for (int i=2;i<=tot;i++)
	{
		if (i&1)
			val[i]=0;
		else
			val[i]=to[i]==1||to[i]==n*2||to[i^1]==1||to[i^1]==n*2?INF:1;
	}
	while(bfs())
	{
		for (int i=s;i<=t;i++)
			cur[i]=head[i];
		ans+=dfs(s, INF);
	}
	printf("%d\n",ans);
	return 0;
}